Se você já realizou operações o suficiente com números flutuantes já deve ter passado com uma situação onde 0.1 + 0.2 = 0.30000000000000004, ou basicamente você tentou comparar os dois e concluindo que 0.1 + 0.2 != 0.3 por exemplo.
Vi algumas pessoas culpando o Javascript ou a linguagem em si, mas na verdade este é um problema que deve ser levado um pouco mais a fundo para entender, tanto que criaram um site explicando o porque disto acontecer.
Neste post pretendo explicar da forma mais concisa que eu conseguir e também como usaram a notação científica (IEEE 754) como referência para a criação de números “flutuantes”.
Números Inteiros
Primeiramente números inteiros que em C sao chamados de long significando que eles possuem 32bit sendo assim
00000000 00000000 00000000 00000000
usados para representar um numero, onde vocês já devem estar acostumados a lidar com números binários.
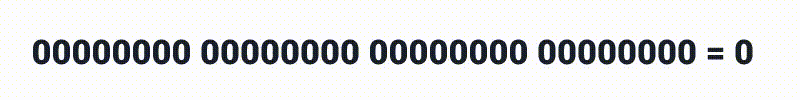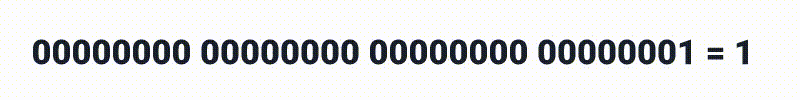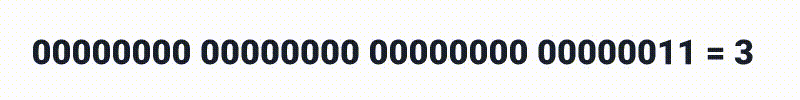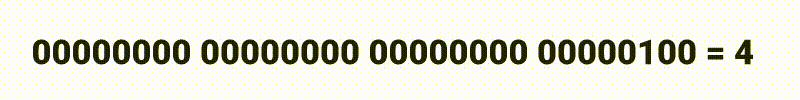
E por ai vai até chegar a 2 bilhões.
Números Decimais
Assim como os numeros inteiros, os números decimais que em C são chamados de float tambem possuem 32bit, porém precisamos definir os decimais também, e como fariamos isso? Se fossemos arquitetar a representação desses numeros, provavelmente fariamos assim:
00000000 00000000 . 00000000 00000000
Simplesmente colocar um ponto decimal no meio, antes do ponto decimal contaríamos da forma usual.
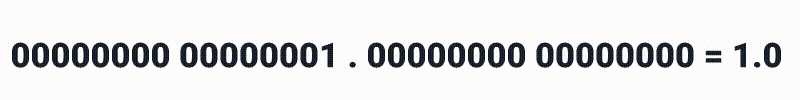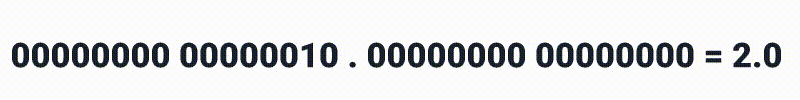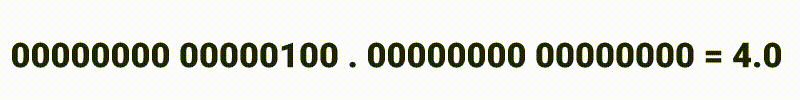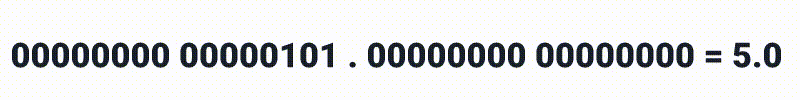
E após o ponto decimal, não temos muitas surpresas também, mas devemos nos atentar que estamos lidando com números binários então ao invés de 10, 100 e 1000 nós teriamos:
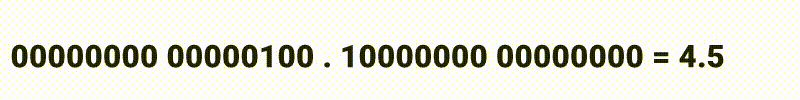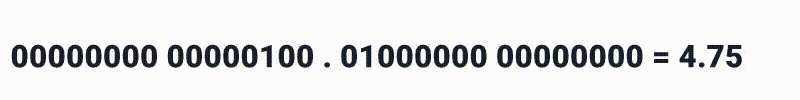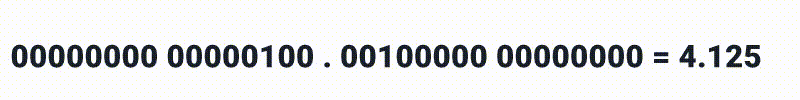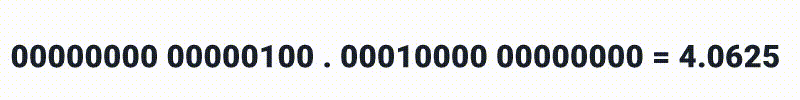
Em qualquer combinação, então por exemplo, 4.75 poderia ser representado destas duas formas:
00000000 00000100 . 11000000 00000000 = 4.75
00000000 00000100 . 01000000 00000000 = 4.75
Mas esta ideia é na verdade horrível, porque detonamos com o tamanho do numero que podemos representar onde antes chegavamos a apróximadamente 2 bilhões, agora só podemos representar numeros até aproximádos 32 mil.
Para a nossa sorte, pessoas mais espertas que nós tiveram a ideia de se inspirar na notação científica e garantir um melhor uso desses 32bits, assim podemos representar números como 23’00 em 2.310⁴ e 0,32 como 3.210⁻³.
Se fossemos representá-los no sistema binário seria algo assim:
11’00 => 1.1x2⁴ seria sua representação em notação cientifica.
0.0101 => 0.01x2⁻³
Esta forma de representação carrega o nome IEEE 754.
O Que Define IEEE 754?
Como de costume, nós receberemos os 32bits, porém como a seguir.
0 00000000 000000000000000000000000
Sendo o primeiro bit o bit do sinal, onde 0 significa que ele é positivo e 1 significa que ele é negativo.
0 00000000 000000000000000000000000 = x
1 00000000 000000000000000000000000 = -x
Os próximos oito bits representam o expoente, sendo então:
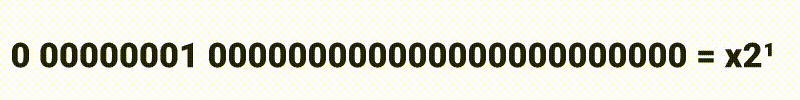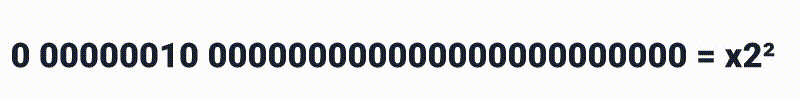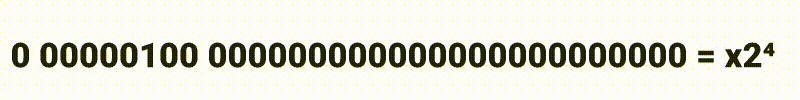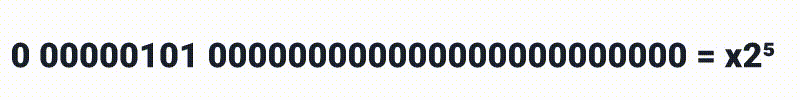
E por ai vai, mas nos atentando que com 8 bits podemos representar números de [255-0], porém também vamos precisar de expoentes negativos, então por este motivo os números são movidos para [128-127], o que significa que ao invés de termos x2³ *como no exemplo anterior, nós teremos **x***2⁽³⁻¹²⁷⁾ e se quisermos que o expoente realmente seja 3, precisamos alterar os bits para 130 como a seguir:
0 10000100 000000000000000000000000 = x*2⁽¹³⁰⁻¹²⁷⁾
Porque 130 - 127 = 3.
E os últimos 23 bits, representa a mantissa. Quando tratamos de notação científica nos queremos definir um dígito, uma vírgula e os decimais, mas com 23 bits podemos definir de 0 ate 2²³ e nao e exatamente disso que precisamos, porque precisamos da mantissa de ir de 1 ate 10, ou em notacao cientifica binaria, de ir de 1 até 2. Podemos tentar novamente fazer oque fizemos da ultima vez e tentar adcionar uma vírgula apos o primeiro bit.
0 10000100 0.0000000000000000000000
Ai podemos definir:
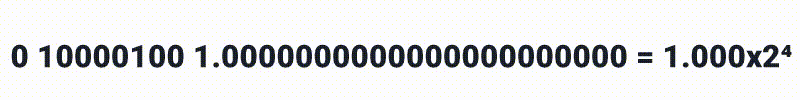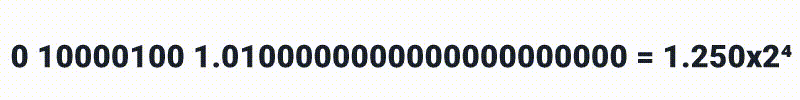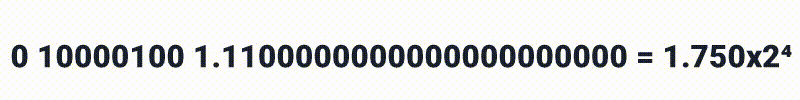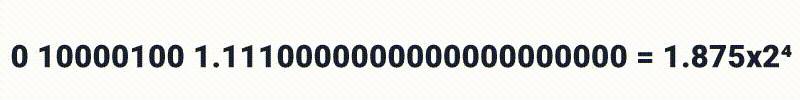
até
0 10000100 1.1111111111111111111111 = 1.999*2⁵
Mas essa soluçao disperdiça um bit armazenamento, as pessoas que fizeram o design desse padrao perceberam que quando estamos lidando com numeros binarios algo acontece que nao acontece em nenhuma outra base.
11’000 1.12⁴ Preste atençao no primeiro digito.
0.0101 1.012⁻³ Por definição, este numero sempre sera não zero.
Mas em binario existe só existe um numero que nao e zero, 1. Ou seja, se sabemos que o primeiro dígito sempre sera 1, nao precisamos guarda-lo, podemos salvar um bit movendo a vírgula para esquerda e deixarmos este numero 1 fixo. Agora nossa mantissa esta entre 1 e 2.
0 10000100 .00000000000000000000000
Por mais que os 23 bits nos deem um alcanse de 0 até 2²³ nós diminuimos para conseguir numeros entre 0 e 1 e entao fixamos o numero 1 para conseguir numeros entre 1 e 2 e esta é a parte principal do padrão IEEE 754, mas para os tais numeros normalizados, Como devem saber neste padrão eles tambem incluem numeros não normalizados, NaN, infinitos e 0 & 0* que talvez eu entre em detalhes num post futuro.
Ta, mas e ai?
Bom, agora que sabemos como os numeros flutuantes são armazenados. Podemos resumir que este caso curioso ocorre devido as bases usadas, os computadores não lidam com números da mesma forma que nós lidamos, eles precisam converter para binário e depois para decimal e quando convertemos para a base decimal acabamos tendo que lidar com algumas “sobras”. o padrão IEEE dita que todas as operações devem ser arredondadas de forma exata, isso significa que todos os resultados devem ser computados de forma exata e então arredondados, e durante essa conversão perdemos essa precisão devido a isso, o que a representação IEEE certifica é que este arredondamento esteja dentro de um certo limite.
Como podemos ver a seguir usando uma ferramenta de conversão.
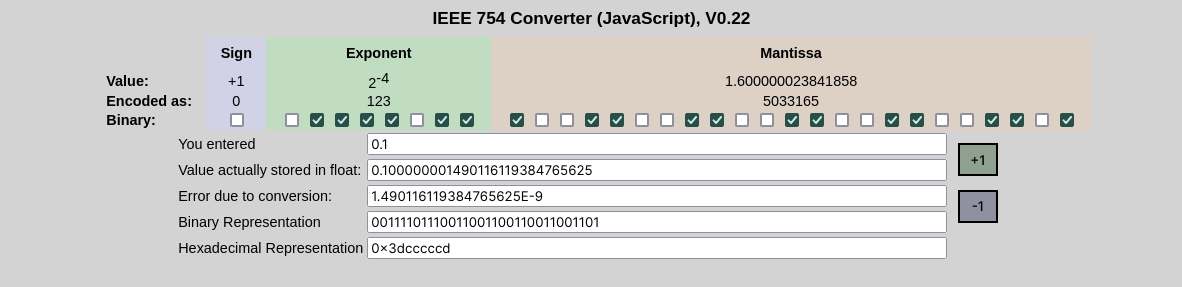
(Ferramenta usada: https://www.h-schmidt.net/FloatConverter/IEEE754.html)
Referências:
What Every Computer Scientist Should Know About Floating-Point Arithmetic
An Introdution to Floating Point by Jeff Arnold
